WHAT IS LINKED LIST
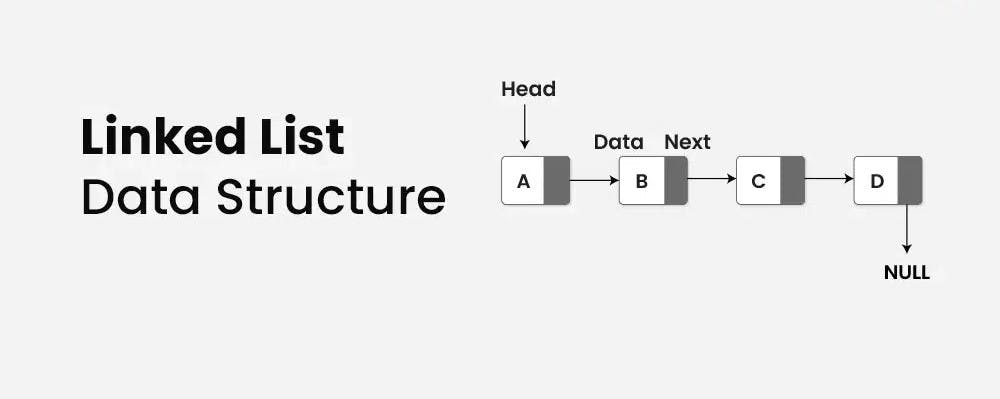
A linked list is a fundamental data structure in computer science. It consists of nodes where each node contains data and a reference (link) to the next node in the sequence. This allows for dynamic memory allocation and efficient insertion and deletion operations compared to arrays.
DIFFRENCE BETWEEN LINKED LIST AND ARRAYS ?
Linked List:
Data Structure: Non-contiguous
Memory Allocation: Dynamic
Insertion/Deletion: Efficient
Access: Sequential
Array:
Data Structure: Contiguous
Memory Allocation: Static
Insertion/Deletion: Inefficient
Access: Random
TYPES OF LINKED LIST :
1.Singly Linked List 2.Doubly Linked List 3.Circular Linked List 4.Circular Doubly Linked List 5.Header Linked List
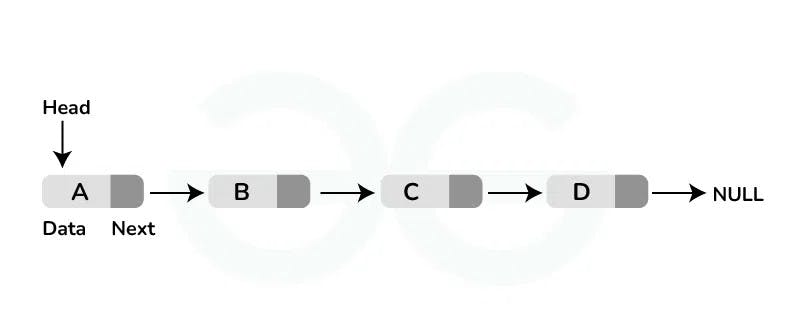
1.Singly Linked List : A singly linked list is a linear data structure in which the elements are not stored in contiguous memory locations and each element is connected only to its next element using a pointer.
2.Doubly Linked List :
Inserting a new node in a doubly linked list is very similar to inserting new node in linked list. There is a little extra work required to maintain the link of the previous node. A node can be inserted in a Doubly Linked List in four ways:
At the front of the DLL.
In between two nodes
After a given node.
Before a given node.
At the end of the DLL.
Insertion at the Beginning in Doubly Linked List:
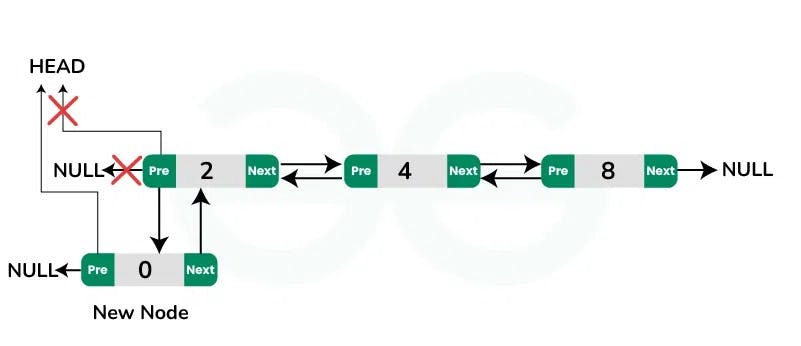
To insert a new node at the beginning of the doubly list, we can use the following steps:
Allocate memory for a new node (say new_node) and assign the provided value to its data field.
Set the previous pointer of the new_node to nullptr.
If the list is empty:
Set the next pointer of the new_node to nullptr.
Update the head pointer to point to the new_node.
If the list is not empty:
Set the next pointer of the new_node to the current head.
Update the previous pointer of the current head to point to the new_node.
Update the head pointer to point to the new_node.
Insertion in between two nodes in Doubly Linked List:
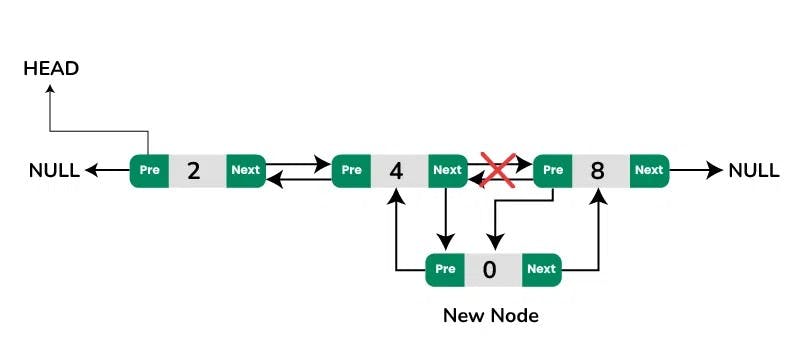
1. Add a node after a given node in a Doubly Linked List:
We are given a pointer to a node as prev_node, and the new node is inserted after the given node. This can be done using the following steps:
Firstly create a new node (say new_node).
Now insert the data in the new node.
Point the next of new_node to the next of prev_node.
Point the next of prev_node to new_node.
Point the previous of new_node to prev_node.
Point the previous of next of new_node to new_node.
Insertion at the End in Doubly Linked List:
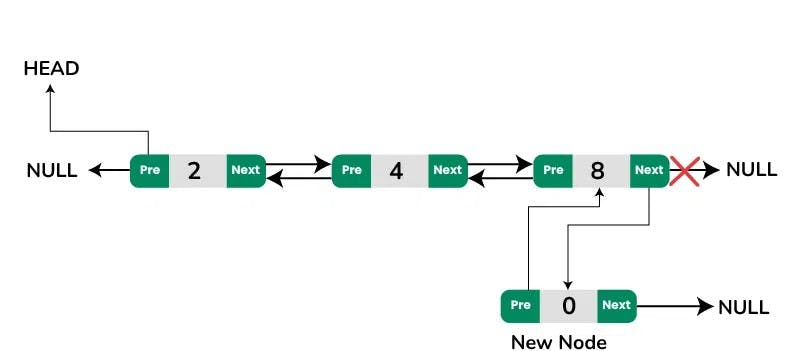
The new node is always added after the last node of the given Linked List. This can be done using the following steps:
Create a new node (say new_node).
Put the value in the new node.
Make the next pointer of new_node as null.
If the list is empty, make new_node as the head.
Otherwise, travel to the end of the linked list.
Now make the next pointer of last node point to new_node.
Change the previous pointer of new_node to the last node of the list.
CIRCULAR LINKED LIST :
The circular linked list is a linked list where all nodes are connected to form a circle. In a circular linked list, the first node and the last node are connected to each other which forms a circle. There is no NULL at the end.
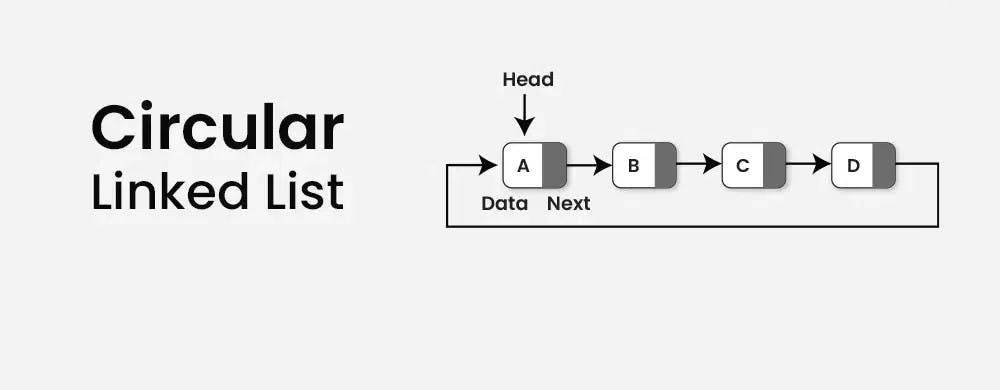
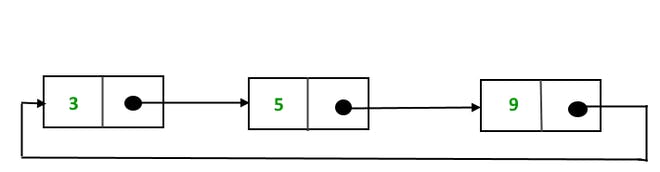
There are generally two types of circular linked lists:
Circular singly linked list: In a circular Singly linked list, the last node of the list contains a pointer to the first node of the list. We traverse the circular singly linked list until we reach the same node where we started. The circular singly linked list has no beginning or end. No null value is present in the next part of any of the nodes.
Circular Doubly linked list: Circular Doubly Linked List has properties of both doubly linked list and circular linked list in which two consecutive elements are linked or connected by the previous and next pointer and the last node points to the first node by the next pointer and also the first node points to the last node by the previous pointer.
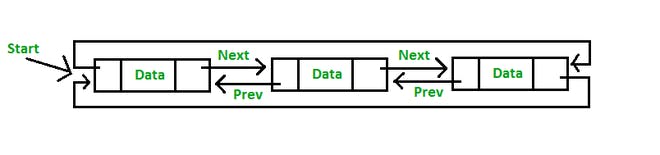
CIRCULAR DOUBLY LINKED LIST :
A circular doubly linked list is defined as a circular linked list in which each node has two links connecting it to the previous node and the next node.
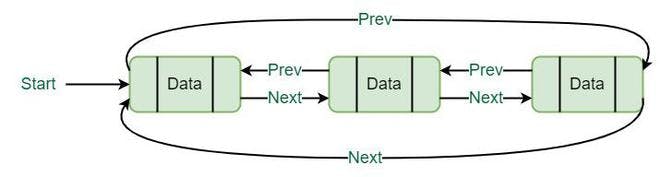
Characteristics of Circular Doubly Linked List :
A circular doubly linked list has the following properties:
Circular: A circular doubly linked list’s main feature is that it is circular in design.
Doubly Linked: Each node in a circular doubly linked list has two pointers – one pointing to the node before it and the other pointing to the node after it.
Header Node: At the start of circular doubly linked lists, a header node or sentinel node is frequently used. This node is used to make the execution of certain operations on the list simpler even though it is not a component of the list’s actual contents.
Applications of Circular Doubly Linked List :
Circular doubly linked lists are used in a variety of applications, some of which include:
Implementation of Circular Data Structures: Circular doubly linked lists are extremely helpful in the construction of circular data structures like circular queues and circular buffers, which are both circular in nature.
Implementing Undo-Redo Operations: Text editors and other software programs can use circular doubly linked lists to implement undo-redo operations.
Music Player Playlist: Playlists in music players are frequently implemented using circular doubly linked lists. Each song is kept as a node in the list in this scenario, and the list can be circled to play the songs in the order they are listed.
Cache Memory Management: To maintain track of the most recently used cache blocks, circular doubly linked lists are employed in cache memory management.
HEADER LINKED LIST :
A header node is a special node that is found at the beginning of the list. A list that contains this type of node, is called the header-linked list. This type of list is useful when information other than that found in each node is needed.
For example, suppose there is an application in which the number of items in a list is often calculated. Usually, a list is always traversed to find the length of the list. However, if the current length is maintained in an additional header node that information can be easily obtained.
Types of Header Linked List
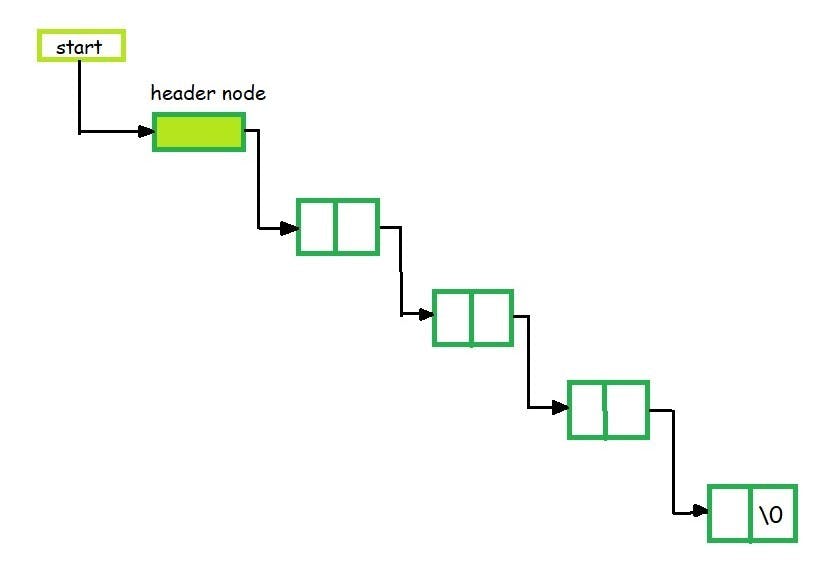
Grounded Header Linked List
It is a list whose last node contains the NULL pointer. In the header linked list the start pointer always points to the header node. start -> next = NULL indicates that the grounded header linked list is empty. The operations that are possible on this type of linked list are Insertion, Deletion, and Traversing.
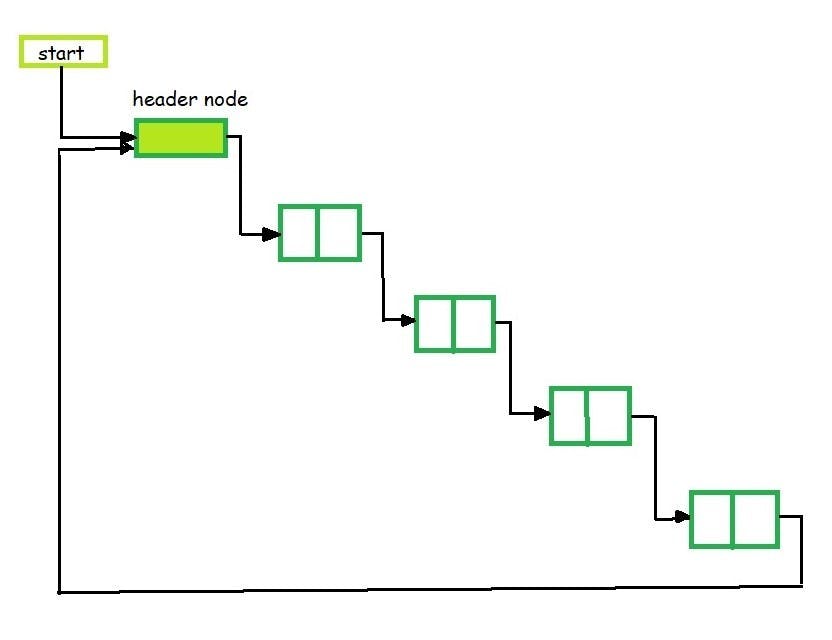
Circular Header Linked List
A list in which last node points back to the header node is called circular linked list. The chains do not indicate first or last nodes. In this case, external pointers provide a frame of reference because last node of a circular linked list does not contain the NULL pointer. The possible operations on this type of linked list are Insertion, Deletion and Traversing.
Applications of Header Linked List
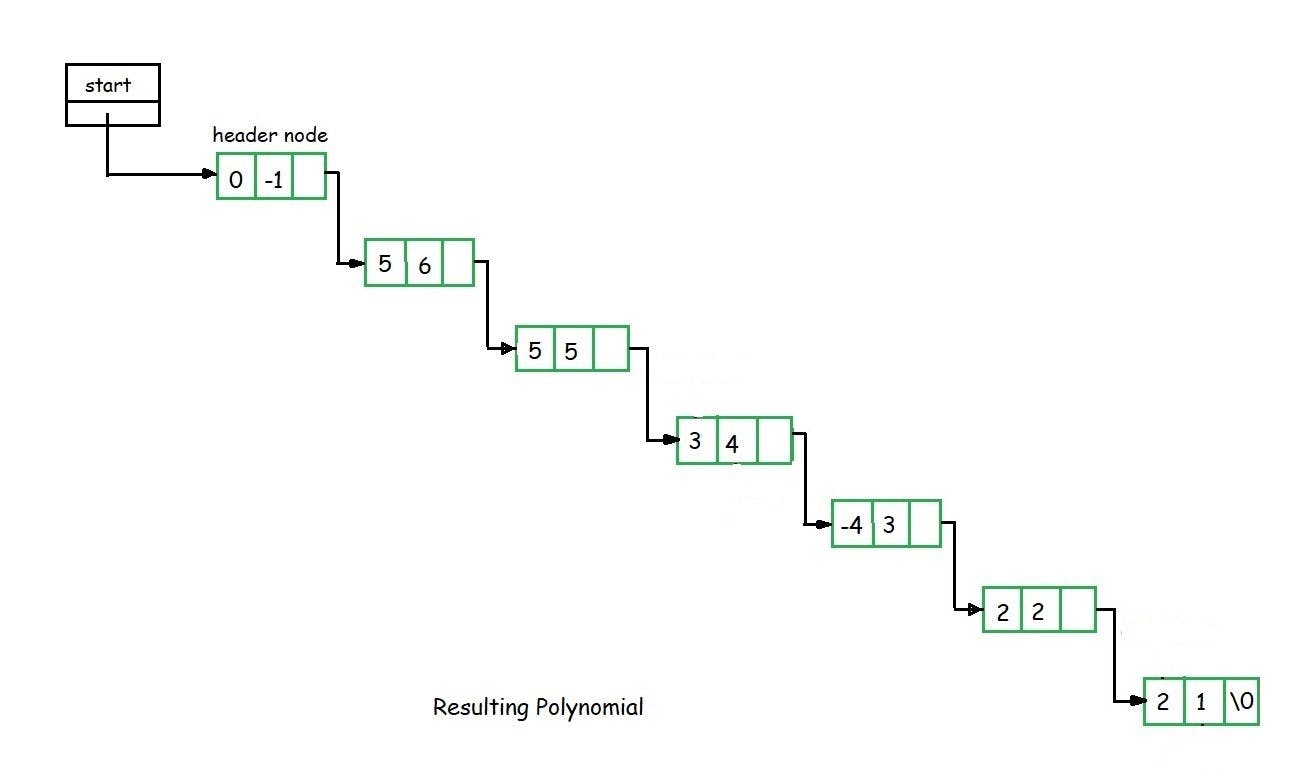
Polynomials
The header linked lists are frequently used to maintain the polynomials in memory. The header node is used to represent the zero polynomial.
Suppose we have
F(x) = 5x5 – 3x3 + 2x2 + x1 +10x0
From the polynomial represented by F(x) it is clear that this polynomial has two parts, coefficient and exponent, where, x is formal parameter. Hence, we can say that a polynomial is sum of terms, each of which consists of a coefficient and an exponent.
The computer implementation requires implementing polynomials as a list of pair of coefficient and exponent. Each of these pairs will constitute a structure, so a polynomial will be represented as a list of structures.
If one wants to represent F(x) with help of linked list then the list will contain 5 nodes. When we link each node we get a linked list structure that represents polynomial F(x).
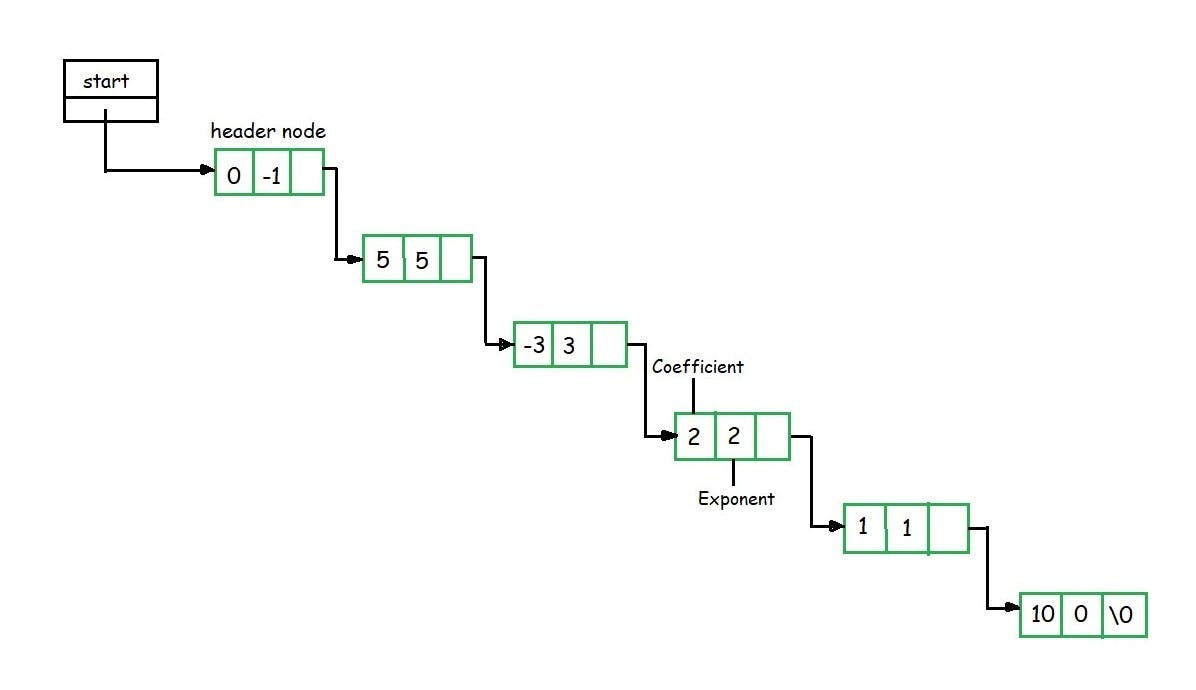
Addition of polynomials
To add two polynomials, we need to scan them once.
If we find terms with the same exponent in the two polynomials, then we add the coefficients, otherwise, we copy the term of larger exponent into the sum and go on.
When we reach at the end of one of the polynomial, then remaining part of the other is copied into the sum.
Suppose we have two polynomials as illustrated and we have to perform addition of these polynomials.
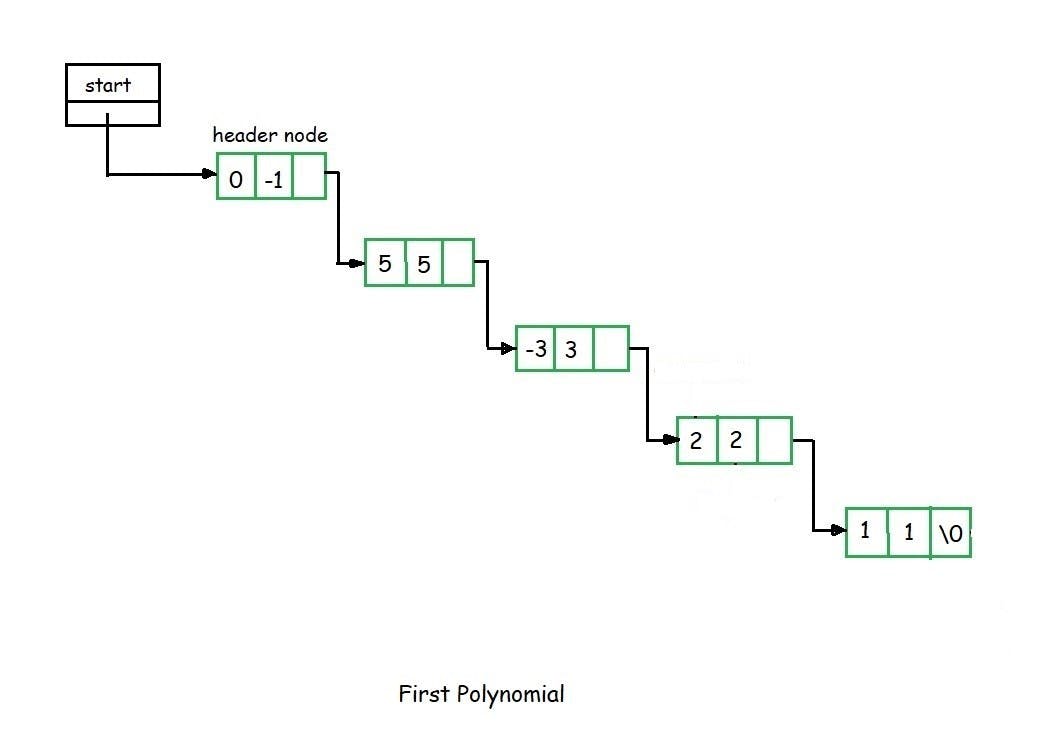
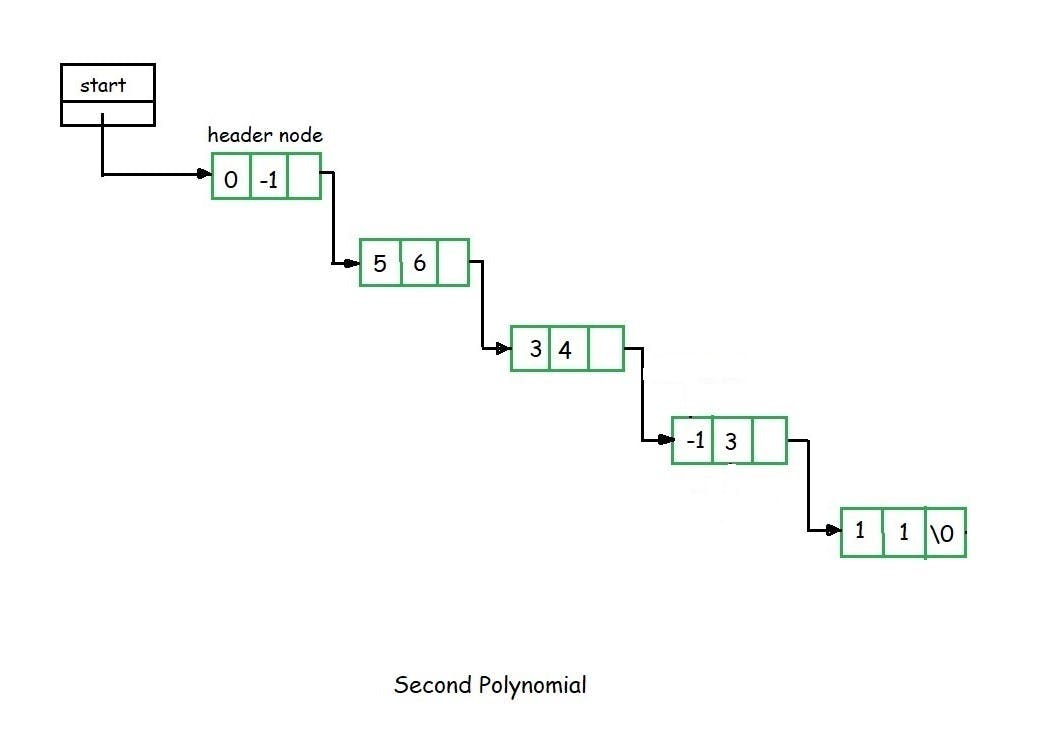
When we scan first node of the two polynomials, we find that exponential power of first node in the second polynomial is greater than that of first node of the first polynomial.
Here the exponent of the first node of the second polynomial is greater hence we have to copy first node of the second polynomial into the sum.
Then we consider the first node of the first polynomial and once again first node value of first polynomial is compared with the second node value of the second polynomial.
Here the first node exponent value of the first polynomial is greater than the second node exponent value of the second polynomial. We copy the first node of the first polynomial into the sum.
Now consider the second node of the first polynomial and compare it with the second node of the second polynomial.
Here the exponent value of the second node of the second polynomial is greater than the second node of the first polynomial, hence we copy the second node of the second list into the sum.
Now we consider the third node exponent of the second polynomial and compare it with second node exponent value of the first polynomial. We find that both are equal, hence perform addition of their coefficient and copy in to the sum.
This process continues till all the nodes of both the polynomial are exhausted. For example after adding the above two polynomials, we get the following resultant polynomial as shown.